Основы моделирования нестационарной термоциклической прочности
Основы моделирования нестационарной термоциклической прочности
Расчетные методы анализа прочности реакторного оборудования нередко сталкиваются с ограничениями из-за идеализации схем, условий и свойств материалов. Поэтому для достоверной оценки напряженно-деформированного состояния требуется проведение представительных экспериментальных исследований.
Наиболее эффективны в этом плане модельные стендовые испытания, приближенные к реальным условиям эксплуатации. Для их корректной постановки необходимо соблюдение принципов моделирования — как геометрического, так и физического. Особенно это важно при изучении термической усталости и предельных состояний, вызванных нестационарными тепловыми процессами.
Необходимость представительных экспериментальных работ
Современные численные методы исследования напряженно-деформированного и предельных состояний реакторного оборудования в силу ряда ограничений, определяемых выбором расчетных схем, граничных и начальных условий, идеализацией истории нагружения и свойств материалов, а также невозможности учета при расчетной оценке прочности влияния ряда технологических факторов, не всегда позволяют получить достаточно представительные результаты.
В связи с этим при проектировании сложного и ответственного реакторного оборудования неизбежно возникает вопрос о постановке и проведении представительных экспериментальных работ.
Наиболее приемлемыми в таких случаях оказываются модельные стендовые испытания, обеспечивающие условия нагружения, приближенные к натурным.
Достоверность получаемых в таких испытаниях результатов определяется соблюдением требований моделирования и условий реального нагружения.
В практических случаях полностью удовлетворить подобные условия можно лишь в специально спроектированных исследовательских стендах. Для правильной постановки таких испытаний прежде всего необходимо определиться с условиями моделирования изучаемого процесса.
Моделирование термической усталости
Вопросы моделирования прочности применительно к условиям статического механического нагружения оборудования разработаны к настоящему времени достаточно полно. В тоже время, применительно к случаю нагружения конструкций нестационарными тепловыми процессами, условия моделирования разработаны недостаточно. Поэтому проиллюстрировать принципы определения критериев подобия напряженного и предельных состояний удобнее всего на примере моделирования термической усталости.
При определении принципов постановки экспериментальных работ вопросы моделирования изучаемых процессов занимают определяющее место.
Особенности реализации возможных предельных состояний в высокотемпературных реакторах выдвигают на первый план необходимость разработки принципов моделирования нестационарного термонапряженного состояния и циклической долговечности.
В самом общем случае процесс усталости — есть процесс появления в металле усталостных трещин, обусловленный исчерпанием пластических свойств конструкционного материала за счет неупругого деформирования на фоне коррозионного влияния рабочей среды. Установим определяющие критерии в явлении термической усталости.
При определении принципов постановки экспериментальных работ вопросы моделирования изучаемых процессов занимают определяющее место.
Особенности реализации возможных предельных состояний в высокотемпературных реакторах выдвигают на первый план необходимость разработки принципов моделирования нестационарного термонапряженного состояния и циклической долговечности.
В самом общем случае процесс усталости — есть процесс появления в металле усталостных трещин, обусловленный исчерпанием пластических свойств конструкционного материала за счет неупругого деформирования на фоне коррозионного влияния рабочей среды. Установим определяющие критерии в явлении термической усталости.
Функциональные зависимости
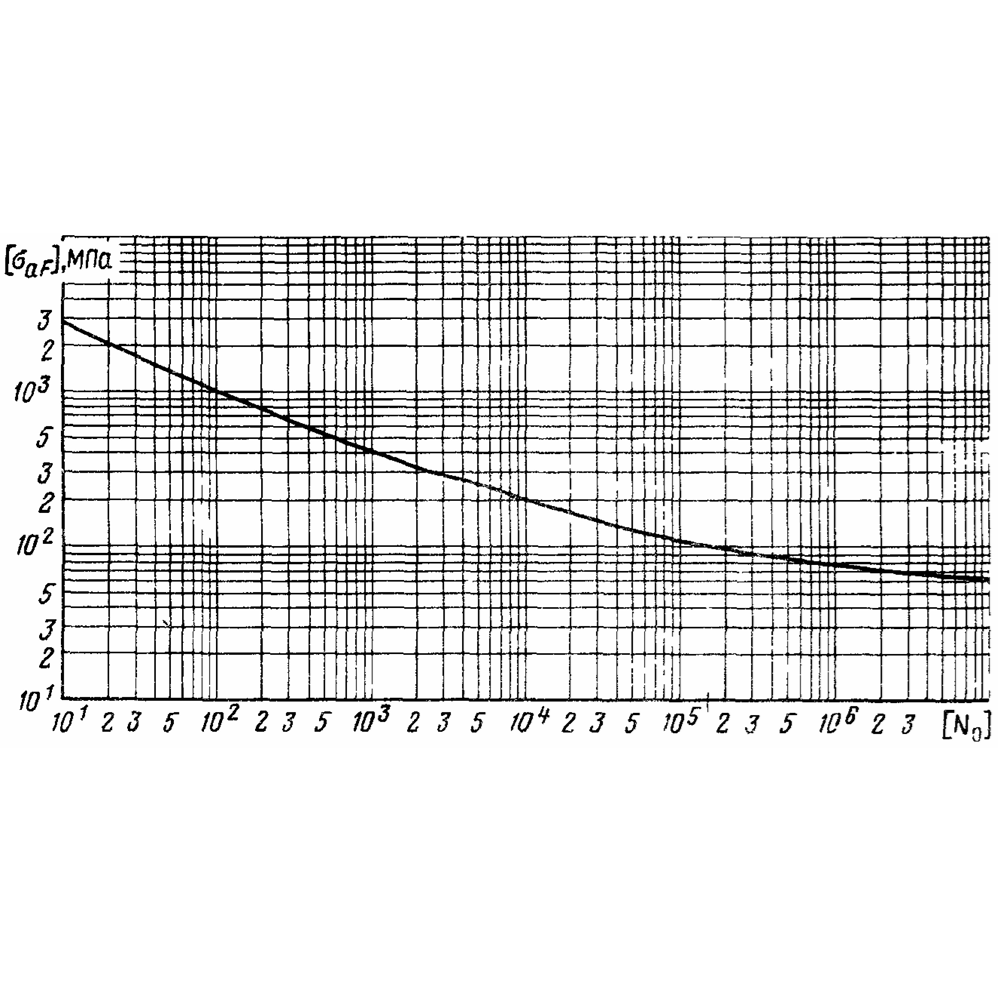
В самом общем виде функциональную зависимость, определяющую связь числа циклов до разрушения с параметрами нагружения, применительно к условиям термической усталости можно записать в виде:
Nо = f (Δt, α, l, a, τ, αt, ε, Kt, ...),
где:
Δt – величина изменения температуры рабочей среды при теплосмене;
α – коэффициент теплоотдачи от рабочей среды к телу;
l – характерный геометрический размер тела;
a – коэффициент теплопроводности конструкционного материала;
τ – характерное время теплосмены;
αt – коэффициент линейного расширения материала тела;
ε – характеристика пластичности материала;
Kt – коэффициент, характеризующий геометрические особенности тела.
Обобщая приведенную запись, можно отметить, что число циклов до разрушения — есть функция, прежде всего, величины нестационарных температурных напряжений в теле конструкции и свойств конструкционного материала, характеризующих его сопротивляемость циклическим нагрузкам.
Нестационарные температурные напряжения, возникающие в конструкции в результате теплосмен и приводящие в конечном итоге к появлению усталостных трещин, определяются градиентом температуры по сечениям тела.
Чтобы подобие нестационарных температурных полей было полным необходимо также соблюдения равенства у натуры и модели критерия, определяющего подобие граничных условий.
В случае, когда теплообмен между телом и рабочей средой происходит по закону Ньютона, то в соответствии с граничными условиями теплообмена 3-го рода, будем иметь следующую зависимость:
dtт/dtср = f(Bi),
где:
dtт – градиент температуры по сечению тела;
dtср – температурный напор;
Bi = (α ⋅ l / λ) – критерий Био;
α – коэффициент теплоотдачи между теплоносителем и телом;
l – характерный геометрический размер;
λ – коэффициент теплопроводности.
Физический смысл этой зависимости состоит в том, что одинаковым значениям критерия Bi отвечают подобные между собой температурные поля. Таким образом, подобие нестационарных температурных полей обеспечивается при условии выполнения равенства в подобных явлениях критериев Био и Фурье, что, в свою очередь, приводит к необходимости соблюдения следующих условий:
• геометрического подобия исследуемых конструкций;
• подобия их физической структуры (конструкционного материала);
• подобия начальных теплофизических состояний;
• подобия тепловых условий на границе взаимодействия конструкции с окружающей ее рабочей средой.
Подобие нестационарных температурных полей в конструкции и модели еще не означает подобия в них нестационарных температурных напряжений. Это видно из следующих рассуждений. В общем случае выражение для нестационарных температурных напряжений можно записать в виде
σt = σ* [(αt ⋅ E ⋅ ΔT) / (1– μ)] Kф,
где:
αt – коэффициент линейного расширения материала;
σ* = f (Bi, Fo) – коэффициент, учитывающий реальные условия теплообмена;
Kф – коэффициент, учитывающий геометрические и физические особенности рассматриваемого сечения тела;
αt – интервал изменения температуры теплоносителя при теплосмене.
Таким образом безразмерный комплекс De = (αt ⋅ Δt) – есть критерий подобия в натурном и модельном объекте температурной деформации.
Если модель геометрически подобна натурному изделию (т.е. Кф = idem) и обе они изготовлены из одного конструкционного материала (т.е. Е = idem, μ = idem), то получаются наиболее простые условия моделирования нестационарных температурных деформаций, сводящиеся к удовлетворению равенства у натуры и модели критериев Bi и Fo, а также величины изменения температуры среды в процессе теплосмены Δt.
Заметим, что в условиях реальных теплосмен, когда в материале реализуются нестационарные процессы, это обстоятельство необходимо дополнительно учитывать при формировании полного комплекса критериев подобия.
Из выражения критерия Фурье следует, что для соблюдения подобия напряженного состояния нестационарные температурные процессы в модели должны развиваться в l2 раз быстрее, чем в натуре. В то же время, характерные для высоких температур реологические процессы в конструкционном материале (ползучесть или релаксация) не зависят от геометрического масштаба и реализуются в натурном изделии и в модели во времени одинаково. Таким образом, становится очевидным, что нестационарные тепловые процессы и реологические процессы в материале оказываются в одной модели несовместимыми.
Nо = f (Δt, α, l, a, τ, αt, ε, Kt, ...),
где:
Δt – величина изменения температуры рабочей среды при теплосмене;
α – коэффициент теплоотдачи от рабочей среды к телу;
l – характерный геометрический размер тела;
a – коэффициент теплопроводности конструкционного материала;
τ – характерное время теплосмены;
αt – коэффициент линейного расширения материала тела;
ε – характеристика пластичности материала;
Kt – коэффициент, характеризующий геометрические особенности тела.
Обобщая приведенную запись, можно отметить, что число циклов до разрушения — есть функция, прежде всего, величины нестационарных температурных напряжений в теле конструкции и свойств конструкционного материала, характеризующих его сопротивляемость циклическим нагрузкам.
Нестационарные температурные напряжения, возникающие в конструкции в результате теплосмен и приводящие в конечном итоге к появлению усталостных трещин, определяются градиентом температуры по сечениям тела.
Чтобы подобие нестационарных температурных полей было полным необходимо также соблюдения равенства у натуры и модели критерия, определяющего подобие граничных условий.
В случае, когда теплообмен между телом и рабочей средой происходит по закону Ньютона, то в соответствии с граничными условиями теплообмена 3-го рода, будем иметь следующую зависимость:
dtт/dtср = f(Bi),
где:
dtт – градиент температуры по сечению тела;
dtср – температурный напор;
Bi = (α ⋅ l / λ) – критерий Био;
α – коэффициент теплоотдачи между теплоносителем и телом;
l – характерный геометрический размер;
λ – коэффициент теплопроводности.
Физический смысл этой зависимости состоит в том, что одинаковым значениям критерия Bi отвечают подобные между собой температурные поля. Таким образом, подобие нестационарных температурных полей обеспечивается при условии выполнения равенства в подобных явлениях критериев Био и Фурье, что, в свою очередь, приводит к необходимости соблюдения следующих условий:
• геометрического подобия исследуемых конструкций;
• подобия их физической структуры (конструкционного материала);
• подобия начальных теплофизических состояний;
• подобия тепловых условий на границе взаимодействия конструкции с окружающей ее рабочей средой.
Подобие нестационарных температурных полей в конструкции и модели еще не означает подобия в них нестационарных температурных напряжений. Это видно из следующих рассуждений. В общем случае выражение для нестационарных температурных напряжений можно записать в виде
σt = σ* [(αt ⋅ E ⋅ ΔT) / (1– μ)] Kф,
где:
αt – коэффициент линейного расширения материала;
σ* = f (Bi, Fo) – коэффициент, учитывающий реальные условия теплообмена;
Kф – коэффициент, учитывающий геометрические и физические особенности рассматриваемого сечения тела;
αt – интервал изменения температуры теплоносителя при теплосмене.
Таким образом безразмерный комплекс De = (αt ⋅ Δt) – есть критерий подобия в натурном и модельном объекте температурной деформации.
Если модель геометрически подобна натурному изделию (т.е. Кф = idem) и обе они изготовлены из одного конструкционного материала (т.е. Е = idem, μ = idem), то получаются наиболее простые условия моделирования нестационарных температурных деформаций, сводящиеся к удовлетворению равенства у натуры и модели критериев Bi и Fo, а также величины изменения температуры среды в процессе теплосмены Δt.
Заметим, что в условиях реальных теплосмен, когда в материале реализуются нестационарные процессы, это обстоятельство необходимо дополнительно учитывать при формировании полного комплекса критериев подобия.
Из выражения критерия Фурье следует, что для соблюдения подобия напряженного состояния нестационарные температурные процессы в модели должны развиваться в l2 раз быстрее, чем в натуре. В то же время, характерные для высоких температур реологические процессы в конструкционном материале (ползучесть или релаксация) не зависят от геометрического масштаба и реализуются в натурном изделии и в модели во времени одинаково. Таким образом, становится очевидным, что нестационарные тепловые процессы и реологические процессы в материале оказываются в одной модели несовместимыми.
Моделирование характеристик несущей способности
При исследовании вопроса моделирования предельных пластических состояний, зависящих от характера полей деформаций, циклических и реологических свойств материала, особое значение приобретает правильность моделирования характеристик несущей способности конструкционного материала. Строгое моделирование физических процессов в подобных случаях (особенно в области реализации упругопластических деформаций) представляет собой довольно сложную задачу.
Применительно к рассматриваемому случаю моделирования условий малоциклового пластического разрушения конструкции необходимо обозначенный выше комплекс критериев дополнить условиями подобия критерия малоциклового разрушения. Для решения этой задачи за основу можно принять критериальную зависимость малоцикловой усталости типа Мэнсона-Коффина, которая устанавливает соотношение между исходными пластическими характеристиками конструкционного материала, размахом пластической деформации в цикле нагружения и числом циклов до наступления предельного состояния — появления трещин усталости.
Отметим, что хотя зависимость такого типа является приближенной, однако она правильно отражает зависимость циклической долговечности от свойств материала. А этого достаточно для установления критерия подобия. Пренебрегая влиянием упругой составляющей деформации и принимая во внимание установленный выше критерий De, можно получить соотношение подобия циклической долговечности модели и натуры в виде
[А / De]нат = [A / (De ⋅ Ec ⋅ Kc / μc)]мод,
где:
A – показатель пластичности материала;
Ec = Eнат / Eмод – соотношение модулей упругости материала натуры и модели;
Kc = Кфнат/ Кфмод – соотношение коэффициентов геометрического подобия натуры и модели;
μс = [1 - μс]нат / [1– μс]мод – соотношение коэффициентов Пуассона натуры и модели.
Можно предложить другую запись критерия подобия предельных пластических состояний:
Aмод = Aнат (Ec ⋅ Kc / μc).
Это выражение устанавливает соотношение между исходными характеристиками пластичности материала натурного изделия и модели, при соблюдении которого обеспечивается равенство показателей циклической долговечности.
Применительно к рассматриваемому случаю моделирования условий малоциклового пластического разрушения конструкции необходимо обозначенный выше комплекс критериев дополнить условиями подобия критерия малоциклового разрушения. Для решения этой задачи за основу можно принять критериальную зависимость малоцикловой усталости типа Мэнсона-Коффина, которая устанавливает соотношение между исходными пластическими характеристиками конструкционного материала, размахом пластической деформации в цикле нагружения и числом циклов до наступления предельного состояния — появления трещин усталости.
Отметим, что хотя зависимость такого типа является приближенной, однако она правильно отражает зависимость циклической долговечности от свойств материала. А этого достаточно для установления критерия подобия. Пренебрегая влиянием упругой составляющей деформации и принимая во внимание установленный выше критерий De, можно получить соотношение подобия циклической долговечности модели и натуры в виде
[А / De]нат = [A / (De ⋅ Ec ⋅ Kc / μc)]мод,
где:
A – показатель пластичности материала;
Ec = Eнат / Eмод – соотношение модулей упругости материала натуры и модели;
Kc = Кфнат/ Кфмод – соотношение коэффициентов геометрического подобия натуры и модели;
μс = [1 - μс]нат / [1– μс]мод – соотношение коэффициентов Пуассона натуры и модели.
Можно предложить другую запись критерия подобия предельных пластических состояний:
Aмод = Aнат (Ec ⋅ Kc / μc).
Это выражение устанавливает соотношение между исходными характеристиками пластичности материала натурного изделия и модели, при соблюдении которого обеспечивается равенство показателей циклической долговечности.
Заключение
Сформулированный полный комплекс критериев определяет условия подобия не только таких видов предельного состояния, которые сводятся к реализации усталостных малоцикловых разрушений, но и всех возможных для реальной конструкции при условии, что модель будет выполнена геометрически подобной натурной. В этом случае в модели моделируются поля деформаций, обусловленные не только характером внешних тепловых воздействий и свойствами материала, но и особенностями геометрии конструкции.
Список использованных источников
1. Мэнсон С. Температурные напряжения и малоцикловая усталость. М.: Машиностроение, 1974, 344 с.
2. Махутов Н.А. Деформационные критерии разрушения и расчет элементов конструкций на прочность. М.: Машиностроение, 1981, 272 с.
3. ПНАЭ Г-7-002-86. Нормы расчета на прочность оборудования и трубопроводов атомных энергетических установок.
Статьи
О температурных напряжениях и их влиянии на прочность изделий
Особенности обоснования сейсмостойкости оборудования АЭС
Поверочный расчет зданий и сооружений на контрольное землетрясение
Нормативные требования к численному моделированию физических процессов
Проверка результатов МКЭ анализа
Особенности обоснования прочности оборудования АЭС
Особенности обоснования долговечности оборудования АЭС
Особенности обоснования долговечности оборудования АЭС
Особенности обоснования долговечности оборудования АЭС