О температурных напряжениях и их влиянии на прочность изделий
О температурных напряжениях и их влиянии на прочность изделий
Как температура влияет на прочность материалов?В статье просто и понятно объясняются основные физические принципы, формулы и причины появления термических напряжений и усталостных трещин.
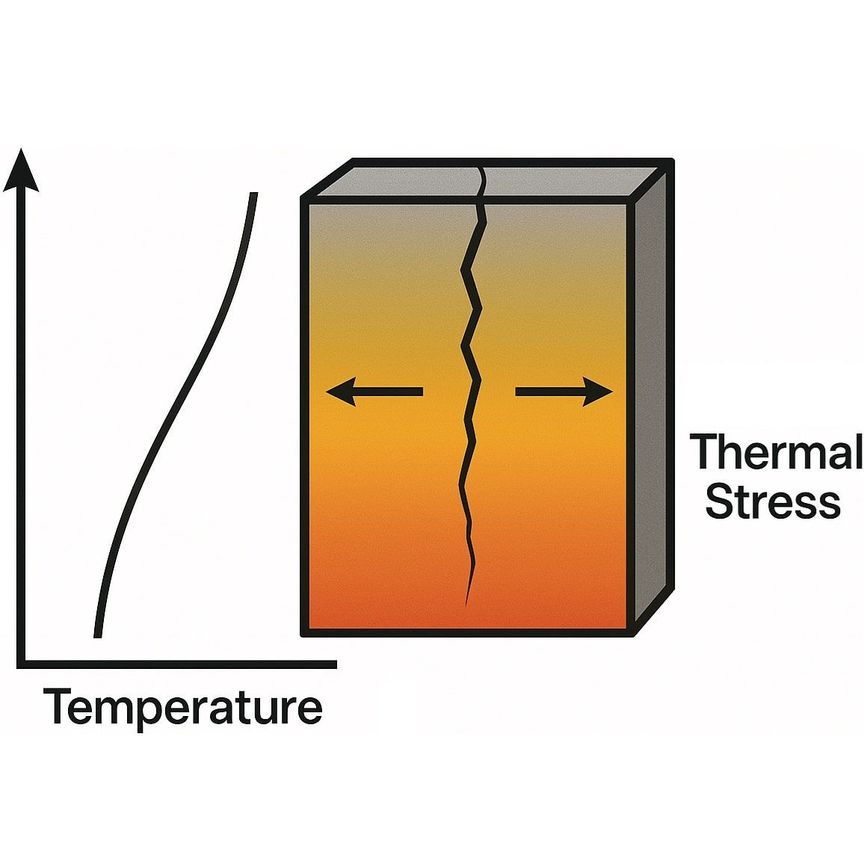
Как возникают температурные напряжения
Размеры физически однородного тела определяются исключительно его среднеинтегральной (среднемассовой) температурой.
Из этого следуют выводы:
• Если в любой точке однородного тела температура одинаковая и равна среднемассовой, то температурные напряжения в теле равны нулю и тело занимает размеры, соответствующие значению его интегральной температуры;
• Температурные напряжения в однородном теле возникают, если в какой-либо точке тела значение температуры будет отличаться от среднеинтегральной;
• Если в любой точке однородного тела температура одинаковая и равна среднемассовой, то температурные напряжения в теле равны нулю и тело занимает размеры, соответствующие значению его интегральной температуры;
• Температурные напряжения в однородном теле возникают, если в какой-либо точке тела значение температуры будет отличаться от среднеинтегральной;
• Температурные напряжения могут возникнуть в теле и при однородном температурном поле, если в теле имеются области физической неоднородности или с различными значениями коэффициента температурного удлинения, или с различным значением модуля упругости.
• Величина температурных напряжений в теле с неоднородной температурой может быть больше определенной по формуле, если на них наложатся напряжения, обусловленные геометрическими неоднородностями конструкции (концентраторы напряжений), которые должны определяться и учитываться отдельно;
• Если значение температуры в точке тела меньше среднеинтегральной, то в этой точке будут возникать растягивающие (принято считать их положительными) напряжения, в противном случае сжимающие (принято считать их отрицательными).
Формула для определения температурных напряжений:
σ = α · E · (Tинт – Ti) / (1 – μ),
где:
где:
α – коэффициент температурного расширения тела;
Е – модуль упругости (модуль Юнга), определяющий связь между величиной деформирования материала и возникающими при этом напряжениями;
Тi – значение температуры в i-ой точке тела;
Тинт – интегральная (среднеобъемная) температура тела;
μ – коэффициент Пуассона, определяющий величину напряжений в объемном теле.
Е – модуль упругости (модуль Юнга), определяющий связь между величиной деформирования материала и возникающими при этом напряжениями;
Тi – значение температуры в i-ой точке тела;
Тинт – интегральная (среднеобъемная) температура тела;
μ – коэффициент Пуассона, определяющий величину напряжений в объемном теле.
Включаем воображение: как мысленный эксперимент помогает понять температурные напряжения
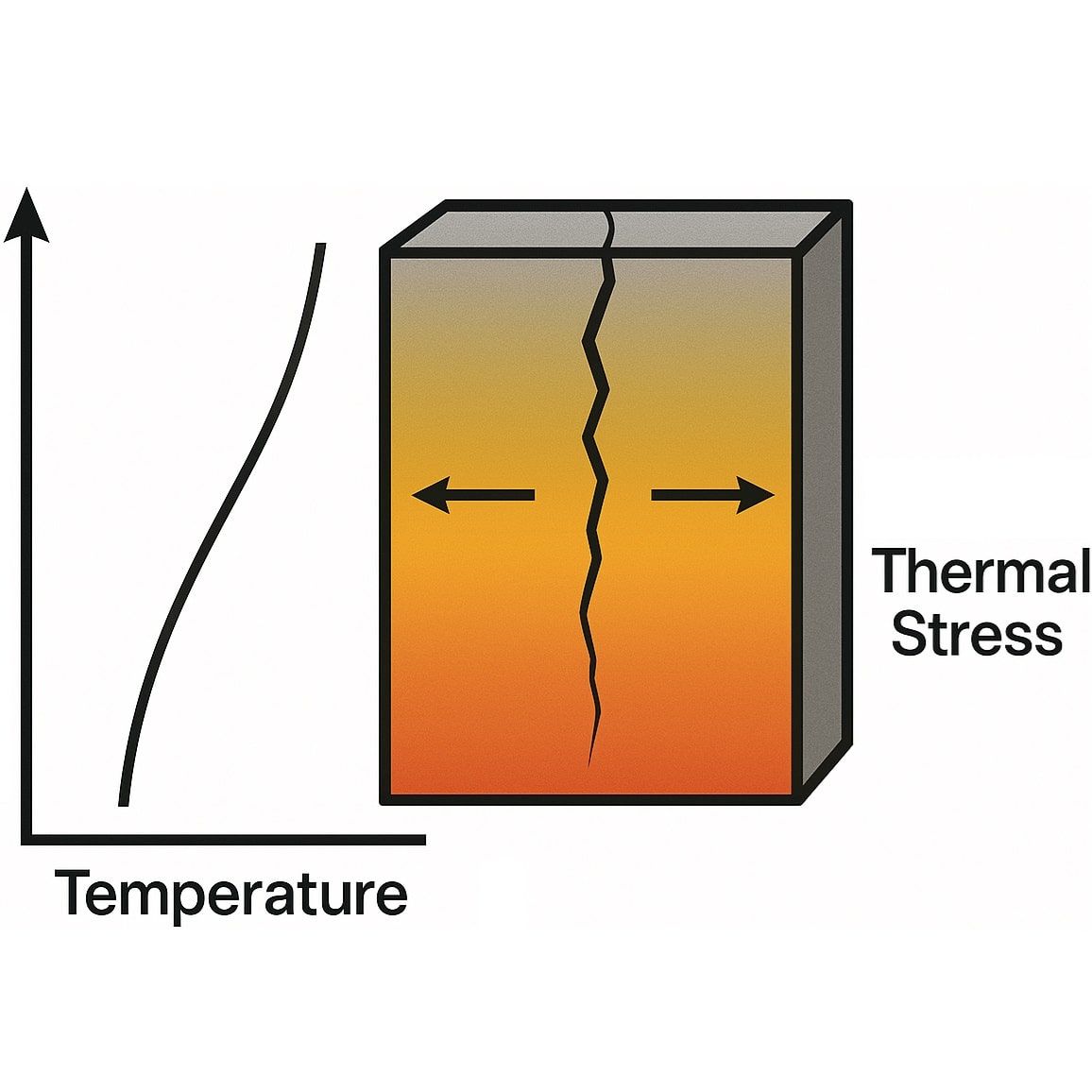
Понять природу температурных напряжений просто, если представить, что мы мысленно «отделяем» небольшой слой материала с температурой Ti от остального тела, которое нагрето до температуры Tинт.
Если температура слоя Тi меньше, чем Tинт, то этот холодный слой в свободном состоянии хотел бы сжаться. Но так как он остается частью более теплого тела, которое его «удерживает» в растянутом состоянии, в этом слое возникают растягивающие напряжения.
Наоборот, если температура слоя Тi выше, чем у остального тела Tинт, то он стремился бы расшириться, но окружающий холодный материал его сдерживает, и возникают сжимающие напряжения.
При этом растягивающие напряжения являются более неблагоприятными для прочности, поскольку вызывают растяжение материала.
Если температура слоя Тi меньше, чем Tинт, то этот холодный слой в свободном состоянии хотел бы сжаться. Но так как он остается частью более теплого тела, которое его «удерживает» в растянутом состоянии, в этом слое возникают растягивающие напряжения.
Наоборот, если температура слоя Тi выше, чем у остального тела Tинт, то он стремился бы расшириться, но окружающий холодный материал его сдерживает, и возникают сжимающие напряжения.
При этом растягивающие напряжения являются более неблагоприятными для прочности, поскольку вызывают растяжение материала.
Что важно учитывать
По своей природе температурные напряжения относятся к разряду деформационных напряжений, поскольку обусловлены тепловыми процессами внутри тела и по величине возможных тепловых деформаций ограничены величиной α · (Tинт – Ti).
При α примерно равном 2 · 10-5 1/оС и максимально возможном диапазоне применения конструкционных материалов (до 1000 оС) получаем максимально возможную реализуемую температурную относительную деформацию, не превышающую 2%.
При этом для большинства используемых пластичных конструкционных сталей деформация разрушения лежит в диапазоне от 20 до 40%.
Иными словами, для пластичных материалов максимально возможные однократные тепловые воздействия не могут вызвать их разрушение.
По этой причине однократные тепловые воздействия, либо воздействия с малой повторяемостью, для подавляющего большинства конструкционных материалов в температурном диапазоне их применения не представляют опасности.
Однако, для некоторых хрупких конструкционных материалов (например чугун и стекло) или материалов, которые могут «охрупчиваться» в процессе эксплуатации, (например под действием облучения), однократные тепловые воздействия уже нельзя игнорировать при выполнении расчетов конструкций на прочность наряду с напряжениями механической природы.
Циклическое нагружение температурными воздействиями
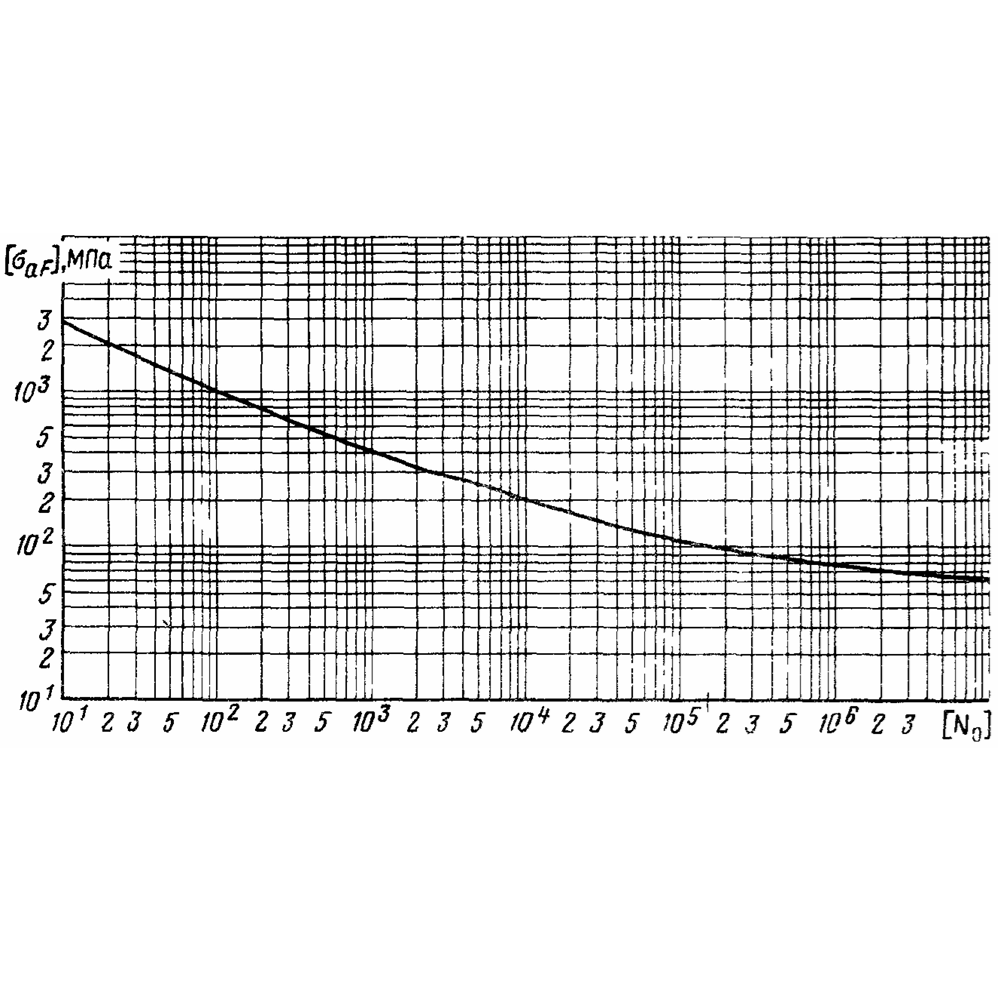
Как показал опыт, многократно повторяющиеся (циклические) температурные напряжения могут вызвать повреждение металла конструкций с развитием усталостных трещин.
Момент образования в металле усталостных трещин (видимых невооруженным взглядом, т.е. размером от 0,5 до 2 мм) для оборудования АЭС рекомендуется определять расчетом циклической прочности — раздел 5.6 «Норм расчета на прочность оборудования и трубопроводов АЭУ» ПНАЭ Г‑7‑002‑86.
Учитывая громоздкость таких зависимостей и самой процедуры определения циклических напряжений, в настоящее время применяются специализированные расчетные программы.
Сам факт появления усталостных трещин определяется в настоящее время нормативными документами прочности как «браковочный» признак, не разрешающий дальнейшую работу конструкции.
Момент образования в металле усталостных трещин (видимых невооруженным взглядом, т.е. размером от 0,5 до 2 мм) для оборудования АЭС рекомендуется определять расчетом циклической прочности — раздел 5.6 «Норм расчета на прочность оборудования и трубопроводов АЭУ» ПНАЭ Г‑7‑002‑86.
Учитывая громоздкость таких зависимостей и самой процедуры определения циклических напряжений, в настоящее время применяются специализированные расчетные программы.
Тем не менее, для осознанного применения этого метода следует иметь в виду основные физические представления, на основе которых разработан метод. Они достаточно простые и заключаются в следующем:
1. Однократные температурные напряжения не представляют опасности для пластичных конструкционных материалов. Тем не менее, циклическое повторное нагружение конструкции может со временем привести к появлению усталостных трещин.
Многочисленные исследования конструкционных материалов показали, что время до появления усталостных трещин находится в прямой зависимости от величины пластичности конструкционного материала и в обратной зависимости от величины циклической деформации в цикле нагружения.
2. Циклические напряжения в разных режимах нагружения конструкции могут быть разными. При этом, на момент появления трещины практически не влияет последовательность чередования циклов с разной величиной напряжений. В большей степени имеет значение общее количество циклов с наибольшими и меньшими по величине значениями.
Многочисленные исследования конструкционных материалов показали, что время до появления усталостных трещин находится в прямой зависимости от величины пластичности конструкционного материала и в обратной зависимости от величины циклической деформации в цикле нагружения.
2. Циклические напряжения в разных режимах нагружения конструкции могут быть разными. При этом, на момент появления трещины практически не влияет последовательность чередования циклов с разной величиной напряжений. В большей степени имеет значение общее количество циклов с наибольшими и меньшими по величине значениями.
Для учета этого, анализу подвергают имеющую циклограмму изменения напряжений за всю историю нагружения, последовательно выделяя количество нагружений с разными размахами напряжений.
3. Температурные напряжения определяют по температурным полям, полученным при решении задачи нестационарной теплопроводности. При этом главной задачей является определение циклов изменения градиентов температуры в исследуемых точках конструкции.
3. Температурные напряжения определяют по температурным полям, полученным при решении задачи нестационарной теплопроводности. При этом главной задачей является определение циклов изменения градиентов температуры в исследуемых точках конструкции.
Также важно помнить, что следует рассматривать напряжения с учетом знака, так как это необходимо для правильного определения размахов и амплитуд в цикле изменения напряжений.
Список использованных источников1. Мэнсон С. Температурные напряжения и малоцикловая усталость. М.: Машиностроение, 1974, 344 с.2. Махутов Н.А. Деформационные критерии разрушения и расчет элементов конструкций на прочность. М.: Машиностроение, 1981, 272 с.3. ПНАЭ Г-7-002-86. Нормы расчета на прочность оборудования и трубопроводов атомных энергетических установок.
Остались вопросы? Наши специалисты на связи

+7 (982) 080-34-11
Ежедневно с 09:00 до 20:00